Zawarte tutaj wyprowadzenia i zależności dotyczą analizy obwodów prądu przemiennego w stanie ustalonym. Wszystkie sygnały są przebiegami sinusoidalnymi o jednakowej częstotliwości, mogą różnić się jedynie przesunięciem fazowym.

Teoria:

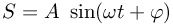
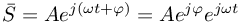
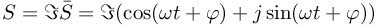
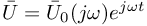
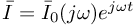
Przed przystąpieniem do obliczeń rzeczywistą postać sygnału: 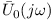zastępujemy notacją zespoloną postaci: A zatem sygnał rzeczywisty jest częścią urojoną z sygnału w postaci zespolonej: Wprowadzona, z pozoru sztuczna notacja, poprzez dopisanie dodatkowego czynnika urojonego zdecydowanie upraszcza obliczenia, pozwalając na stosowanie rachunku liczb zespolonych. Napięcie i prąd w tej notacji mają postać: gdzie oraz 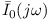są amplitudami zespolonymi napięcia i prądu zależnymi od częstości 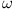i fazy 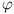sygnału. Warto zauważyć, że czynnik 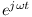dający zależność od czasu, wchodzący w skład liniowych równań opisujących obwody liniowe można z powodzeniem uprościć, gdyż występuje w każdym składniku każdego równania. W efekcie od razu można każde źródło napięcia bądź prądu zastąpić odpowiednią wartością amplitudy zespolonej i dalej liczyć zwykłe równania algebraiczne. Końcowy wynik łatwo zamienić znowu na postać czasową, mnożąc go przez wektor wirujący 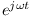i licząc część urojoną z tak powstałego wyrażenia.

Rezystory

Rezystory w obwodzie prądu przemiennego są odpowiedzialne za rozpraszanie mocy czynnej. Nie magazynują energii elektrycznej. Ich impedancja zespolona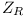 jest równa rezystancji R.

Kondensatory

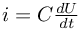
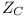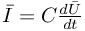
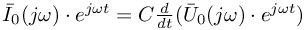
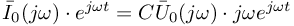
Kondensatory mogą pobierać, magazynować a następnie oddawać energię elektryczną. Prąd płynący przez kondensator spełnia zależność: 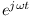gdzie C jest pojemnością kondensatora. Jednostką pojemności jest 1F (Farad) Na podstawie powyższego wzoru oraz wprowadzonych wcześniej zależności wyprowadzamy wzór na impedancję kondensatora : Po uproszczeniu stronami przez wektor wirujący otrzymujemy:

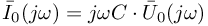
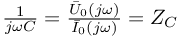
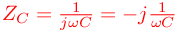
Cewki

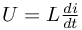
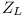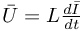
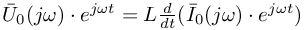
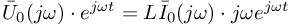
Cewki podobnie jak kondensatory mogą pobierać, magazynować a następnie oddawać energię elektryczną. Napięcie na cewce spełnia zależność: 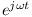gdzie L jest indukcyjnością cewki. Jednostką indukcyjności jest 1H (Henr). Na podstawie powyższego wzoru oraz wprowadzonych wcześniej zależności wyprowadzamy wzór na impedancję cewki : Po uproszczeniu stronami przez wektor wirujący otrzymujemy:

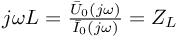
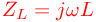
Przykłady:

Przykład 1:

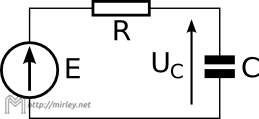
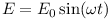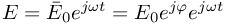
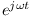W obwodzie z rysunku 1 zadaniem jest obliczenie napięcia na kondensatorze. Napięcie zasilające jest równe: . Zapisujemy źródło napięcia w postaci zespolonej: W dalszej części obliczeń pomijamy wektor wirujący , uwzględniając w obliczeniach tylko amplitudę zespoloną 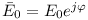. Po dokonaniu obliczeń pomnożymy wynik przez wektor wirujący i wyliczymy część urojoną rozwiązania, uzyskując wynik końcowy. W naszym przykładzie 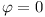a zatem 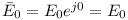. 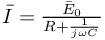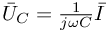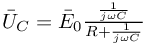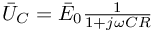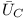Korzystając z Prawa Ohma mamy: oraz: Łącząc dwa powyższe wzory otrzymujemy: Mnożymy przez wektor wirujący 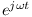oraz korzystamy z faktu że otrzymując: a następnie sprowadzamy do postaci wykładniczej: Ostateczny wynik w postaci rzeczywistej otrzymujemy biorąc część urojoną z :

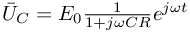
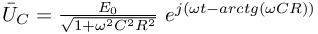
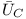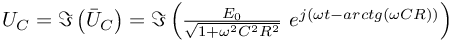
Przykład 2:

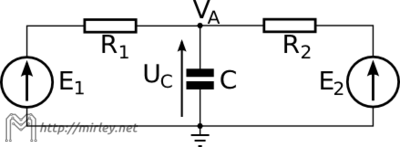
W obwodzie przedstawionym na rysunku 2 zadaniem jest również obliczenie napięcia na kondensatorze. Napięcia zasilające są równe: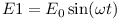 oraz 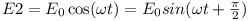. Zapisujemy źródła napięciowe w postaci zespolonej, pomijając wektory wirujące tak jak w poprzednim przykładzie: Korzystamy z metody potencjałów węzłowych i zapisujemy równanie: Dalsza część obliczeń jest analogiczna do tych w pierwszym przykładzie. 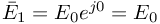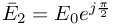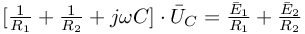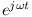Po wyliczeniu szukanej wartości w postaci amplitudy zespolonej, mnożymy całość przez wektor wirujący i bierzemy część urojoną z tego wyrażenia, uzyskując wynik końcowy w postaci rzeczywistej.

Pytania i Komentarze:

comments powered by Disqus